Generando razonamiento matemático escolar a través de ambientes de geometría computacional.
Generando razonamiento matemático escolar a través de ambientes de geometría computacional.

By Yonathan Bonelo Ayala
Profesor de matemáticas
Liceo Benalcázar
Desde un panorama general, en las dos últimas décadas de historia como nación, la educación matemática en Colombia desde sus primeros años de escolaridad, ha propuesto enfrentar distintos problemas de orden académico y curricular en torno a la enseñanza y el aprendizaje, impulsando en cierta medida la necesidad de reformar, o más bien, de lograr construir una propuesta curricular que fuese capaz de soportar un cambio de ruta.
Es por ello que un desafío importante en la enseñanza y el aprendizaje de las matemáticas escolares, es poder estudiar la transición de una explicación / argumento empírico a una prueba matemática aceptable. En investigaciones actuales en educación matemática se ha trabajado mucho para detallar cómo poder facilitar los procesos de generación de conjeturas de los estudiantes, pero todavía hay una brecha en la investigación sobre el proceso de razonamiento de los estudiantes para proporcionar una explicación o demostración matemática, sobre lo que descubren empíricamente.
Tal desafío invita a pensar y a plantearse, que aprender matemáticas desde los primeros años de escolaridad va más allá de memorizar un conjunto de definiciones, algoritmos y técnicas para resolver actividades rutinarias (Benítez ,2006). Es entender las matemáticas no como los resultados de una actividad, sino como la actividad misma; no como un producto, sino como un proceso complejo que alberga tanto los resultados y las técnicas, los interrogantes, las conjeturas y los métodos que en una época dada permiten que un proceso determinado se transforme en un objeto matemático (Recalde ,2017).
La apuesta que hoy planteamos en el Liceo Benalcalcazar es en la promoción del desarrollo de conocimiento y aprendizaje matemático, el cual puede rastrearse mediante los procesos de pensamiento matemático del estudiante, en donde juegan un rol muy importante la construcción de Conjeturas, los procesos de Visualización y la mediación instrumental que enmarcan los ambientes de Geometría Dinámica (DGE), en este caso Geogebra.
Los sistemas de geometría dinámica ayudan a crear un ambiente de aprendizaje donde los estudiantes pueden experimentar, observar la permanencia de las propiedades matemáticas, y verificar las conjeturas mucho más fácilmente que en otros ambientes computacionales y que en el entorno de lápiz y papel. (Marrades & Gutiérrez. 2000, p.95) Geogebra se caracteriza por trabajar con sistemas matemáticos, en este caso un sistema geométrico que está conformado por objetos (puntos, rectas y polígonos), por operaciones (construcciones con regla y compás y las Transformaciones Isométricas en el plano) y por relaciones (paralelismo, pertenencia y perpendicularidad). También cuenta con una fenomenología propia que emerge del ambiente dinámico. Dichos fenómenos que ocurren en la pantalla son el arrastre, el lugar geométrico y la animación que permite ver el proceso de construcción de los objetos geométricos a través del movimiento.
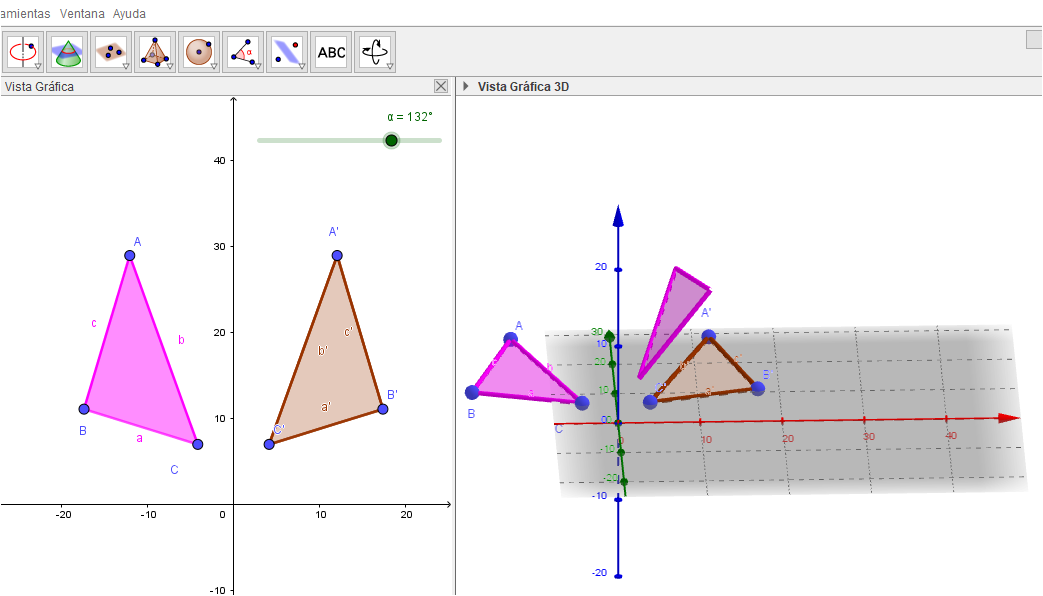
Ahora bien, y particularizando esta propuesta educativa en el liceo que se hace desde y para la educación matemática, se detalla el nuevo realismo matemático que se desarrolla en los ambientes de tecnología computacional, ya que posibilita un abordaje en la investigación para el desarrollo de aprendizajes en la construcción de conjeturas, en particular en la geometría fundamental.
Es por ello que esta propuesta busca incluir el uso de las TIC en el aula de modo que los estudiantes amplíen sus competencias matemáticas, lo cual no ocurre espontáneamente, sino que requiere de ambientes de aprendizaje enriquecidos por situaciones problema significativas y comprensivas, que posibiliten el avance a niveles de competencia más complejos (MEN 2009).
Se pretende la idea de Conjetura ya que este referente hace parte de los procesos generales de la actividad matemática. En Colombia, en particular en los lineamientos curriculares y estándares básicos de competencia en matemáticas se habla de ser Matemáticamente Competente y para lograrlo se deben dominar, conocer, utilizar recursos, procedimientos y procesos, y uno de ellos e indispensable para este desarrollo es el de conjeturar.

